前面我们了解了如何开展机器学习项目,这节课我们来看看深度学习中非常著名的卷积神经网络 CNN。
更新历史
- 2019.10.19: 完成初稿
边缘检测 Edge Detection
我们通过一个边缘检测的例子来说明卷积如何进行计算,如下图所示:
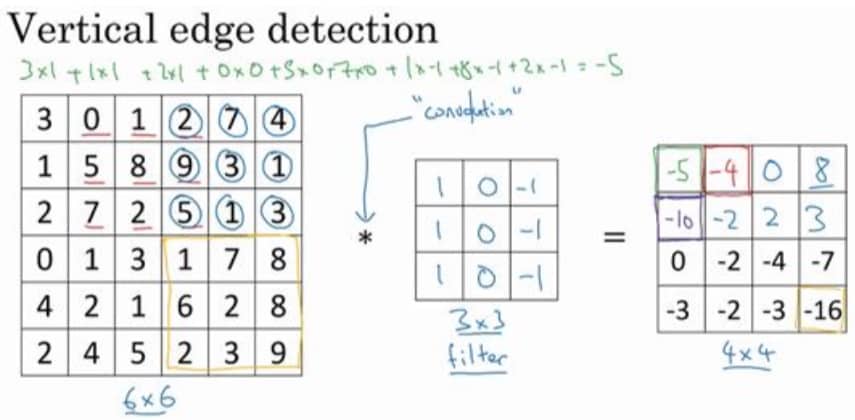
中间的 filter 就是一个垂直方向上的边缘检测过滤器,卷积就是基础的矩阵乘法,这里不再赘述。至于为啥可以做边缘检测,下图是一个很好的说明:
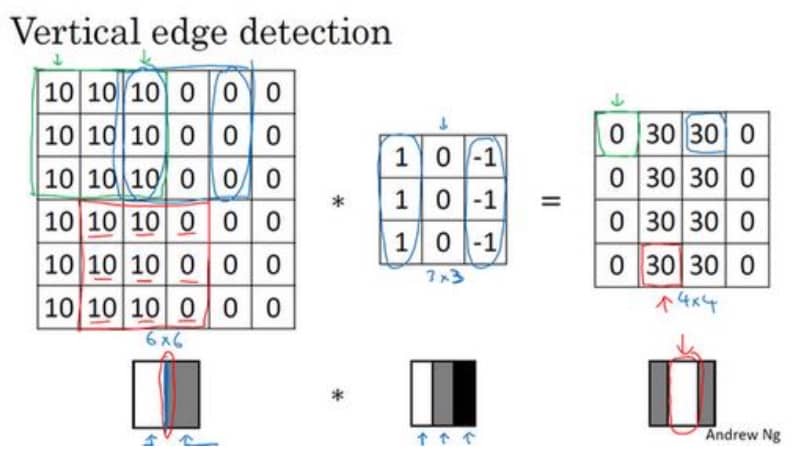
这里的关键在于中间的 filter 矩阵,在深度学习中,这 9 个数字会作为参数,由反向传播算法进行学习。
Padding 与 Stride
这俩概念也很重要,虽然这里不详细介绍,但是需要理解它们在计算中的意义,总结如下:

三维卷积 Convolutions over Volumes
三维卷积能够更好地让我们处理 RGB(或其他多通道)图像,具体如下:
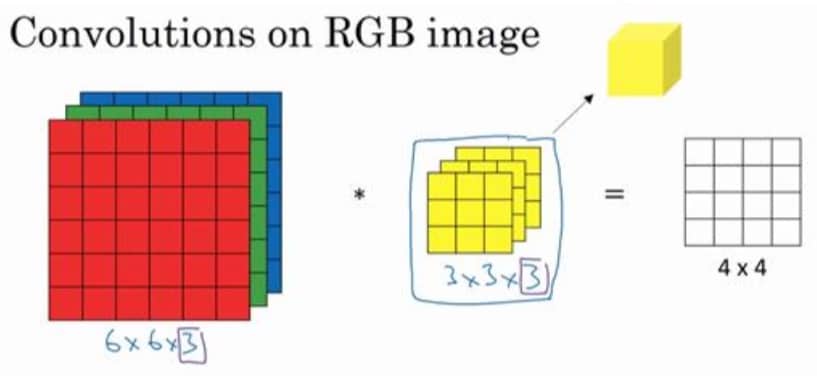
注意,这里我们会每次把整个 3x3x3 矩阵和 RGB 图片的矩阵进行计算,最终得到一个 4x4x1 的矩阵,计算过程如下:
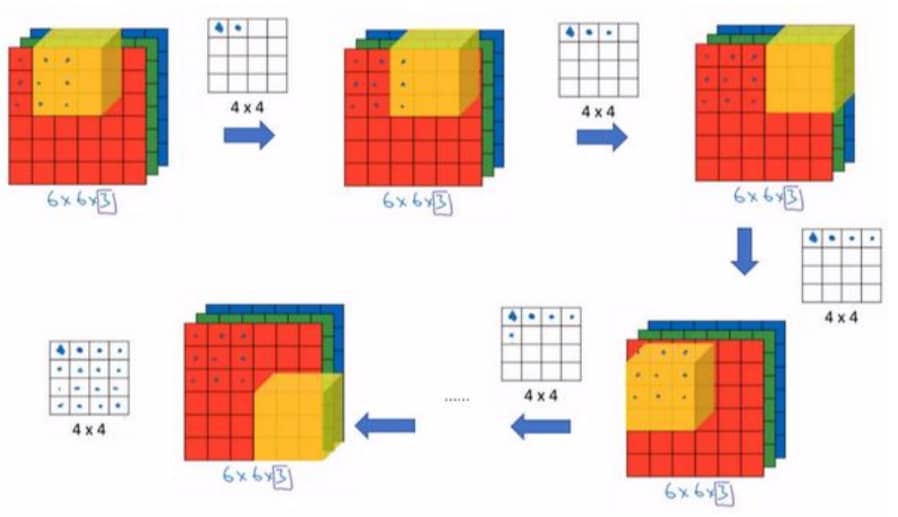
当然,如果我们有多个过滤器,就可以得到多个 4x4 矩阵,这里 $n_c$ 表示通道数目,如下图所示:

单层卷积网络 One Layer of a Convolutional Network
我们现在知道了如何做卷积,但是如果想要组成一个神经网络,还需要加上我们之前的套路:激活函数。这里我们用 ReLU 来做激活函数,可以得到这样一个神经网络
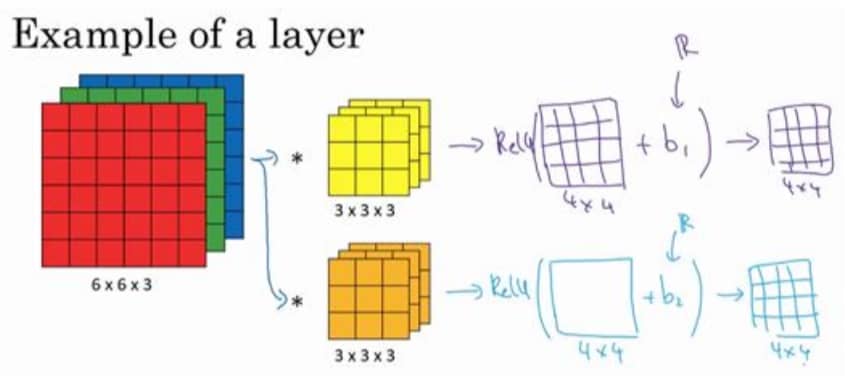
总结下卷积层的公式和参数个数:

简单卷积神经网络实例 A Simple Convolution Network Example
这里我们用一个更加实际的例子来讲解下卷积神经网络,整体如下:

- 第 0 层,我们的图片大小是 39x39,通道数为 3,所以矩阵大小是 39x39x3
- 第 1 层,使用 10 个 3x3 的过滤器来提取特征,padding=0, stride=1,于是最终会得到 37x37x10 的矩阵
- 第 2 层,使用 20 个 5x5 的过滤去来提取特征,padding=0, stride=2,于是最终会得到 17x17x20 的矩阵
- 第 3 层,使用 40 个 5x5 的过滤器,padding=0, stride=2,于是最终会得到 7x7x40=1960 的矩阵
- 最后,我们将这 1960 个参数接入 logistic/softmax 回归单元,就可以完成 二类/多类 的判断
前面我们接触的都是 Convolution(Conv) 层,还有 Pooling(Pool) 层和 Fully Connected(FC) 层,我们也来看看。
池化层 Pooling Layers
池化层通常用来缩减模型大小,提高计算速度,同时提高所提取特征的鲁棒性,如下图所示:
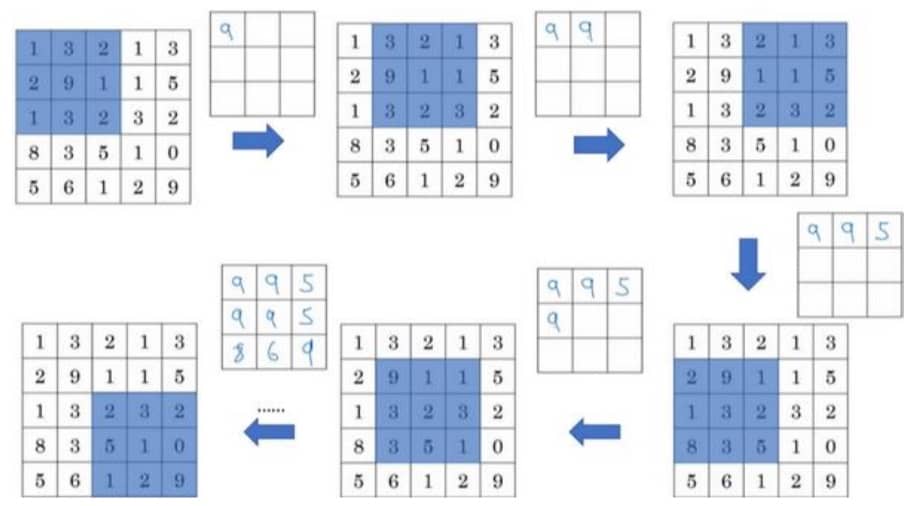
一般来说比较常用的是最大池化,还有一种平均池化(但比较少用)。这是一个静态属性,没有要进行梯度下降学习的内容。接下来我们来看看加上全连接层的卷积神经网络。
卷积神经网络实例 Convolutional Neural Network Example
直接来看看基于 LeNet-5 的一个网络
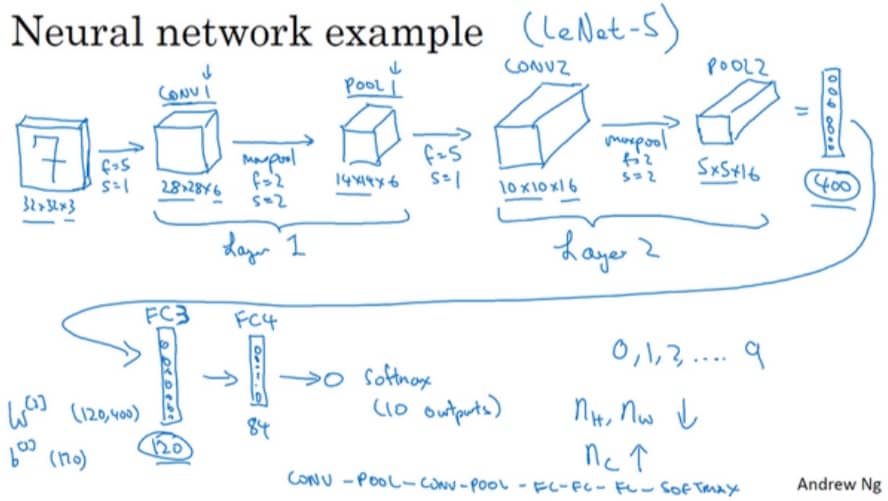
注意,这种网络连接方式是非常经典的,大家可以仔细感受下。另外对应的结构列出表格为:
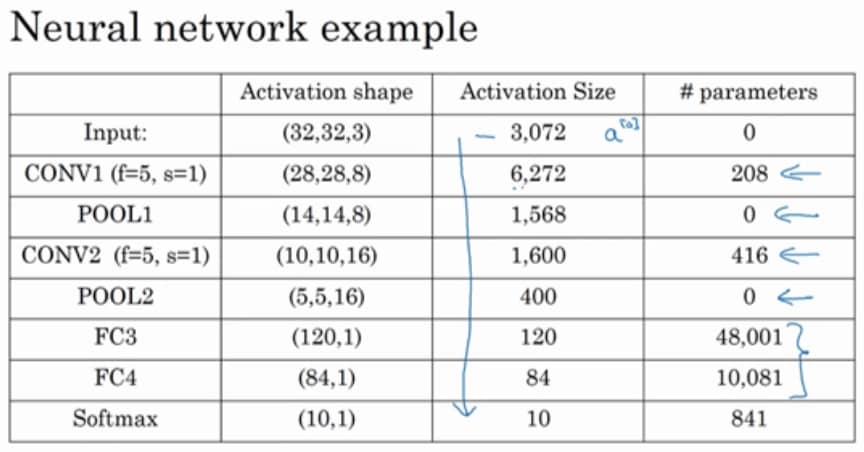
从上表可以知道
- 池化层没有参数
- 卷积层的参数数量与全连接相比少很多
- 激活尺寸逐渐变小(但也不能下降太快)
找到整合基本构造模块最好的方法是大量阅读别人的案例,这样才能找到感觉。
为什么使用卷积 Why Convolutions?
和只用全连接层相比,卷积层的两个主要优势是参数共享和稀疏连接,可以极大减少参数,这样我们的训练集也不用特别大,降低了过拟合。
具体到训练的部分,我们同样有一个花费函数,同样还是用梯度下降。如果用深度框架的化,这些都可以轻松完成。
