【编程起跑线】07 树和图

树和图的问题，说难也难，说简单也简单。难在思路和理解，简单在很多时候可以利用递归得到非常优雅的解法。

---

更新历史

• 2019.08.05：编入新系列
• 2016.01.23：完成初稿

树的概念

树(tree)是一种能够分层存储数据的重要数据结构，树中的每个元素被称为树的节点，每个节点有若干个指针指向子节点。从节点的角度来看，树是由唯一的起始节点引出的节点集合。这个起始结点称为根(root)。树中节点的子树数目称为节点的度(degree)。在面试中，关于树的面试问题非常常见，尤其是关于二叉树(binary tree)，二叉搜索树(Binary Search Tree, BST)的问题。

所谓的二叉树，是指对于树中的每个节点而言，至多有左右两个子节点，即任意节点的度小于等于2。而广义的树则没有如上限制。二叉树是最常见的树形结构。二分查找树是二叉树的一种特例，对于二分查找树的任意节点，该节点存储的数值一定比左子树的所有节点的值大比右子树的所有节点的值小“(与之完全对称的情况也是有效的：即该节点存储的数值一定比左子树的所有节点的值小比右子树的所有节点的值大)。

基于这个特性，二分查找树通常被用于维护有序数据。二分查找树查找、删除、插入的效率都会于一般的线性数据结构。事实上，对于二分查找树的操作相当于执行二分搜索，其执行效率与树的高度(depth)有关，检索任意数据的比较次数不会多于树的高度。这里需要引入高度的概念：对一棵树而言，从根节点到某个节点的路径长度称为该节点的层数(level)，根节点为第0层，非根节点的层数是其父节点的层数加1。树的高度定义为该树中层数最大的叶节点的层数加1，即相当于于从根节点到叶节点的最长路径加1。由此，对于n个数据，二分查找树应该以“尽可能小的高度存储所有数据。由于二叉树第L层至多可以存储 2^L 个节点，故树的高度应在logn量级，因此，二分查找树的搜索效率为O(logn)。

直观上看，尽可能地把二分查找树的每一层“塞满”数据可以使得搜索效率最高，但考虑到每次插入删除都需要维护二分查找树的性质，要实现这点并不容易。特别地，当二分查找树退化为一个由小到大排列的单链表(每个节点只有右孩子)，其搜索效率变为O(n)。为了解决这样的问题，人们引入平衡二叉树的概念。所谓平衡二叉树，是指一棵树的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。通过恰当的构造与调整，平衡二叉树能够保证每次插入删除之后都保持平衡性。平衡二叉树的具体实现算法包括AVL算法和红黑算法等。由于平衡二叉树的实现比较复杂，故一般面试官只会问些概念性的问题。

满二叉树(full binary tree)：如果一棵二叉树的任何结点，或者是叶节点，或者左右子树都存在，则这棵二叉树称作满二叉树。

完全二叉树(complete binary tree)：如果一棵二叉树最多只有最下面的两层节点度数可以小于2，并且最下面一层的节点都集中在该层最左边的连续位置上，则此二叉树称作完全二叉树。

Free tree

指的是相互连接的无环无向图

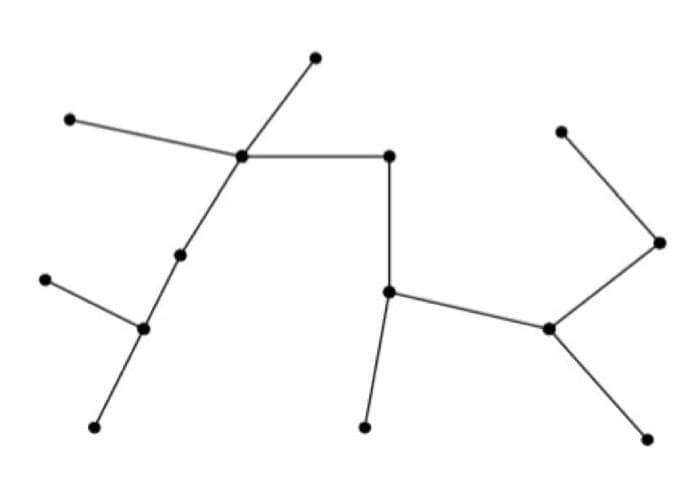
假设 G = (V, E) 是一个无向图，那么下面的语句是等价的：

1. G 是一个 free tree
2. G 中的任意两个节点间都有唯一的一条路径
3. G 是连通的的，但是如果去掉任何一条边，G 就不连通了
4. G 是连通的，并且 $|E|=|V|-1$
5. G 是无环的，并且 $|E|=|V|-1$
6. G 是无环的，但是加入任何一条新的边，就会变成有环的

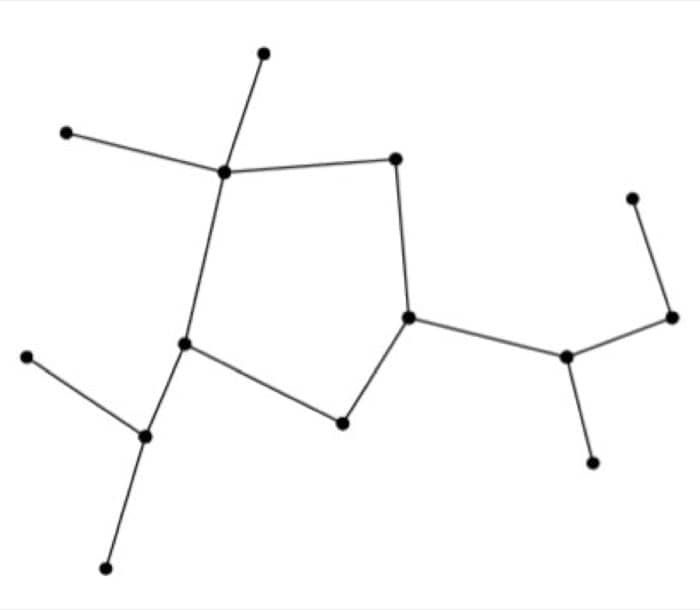
Forest 森林

同样是无环无向图，但不是所有的节点都是连通的

下图中包含一个环，所以不能算是森林：

Rooted Tree

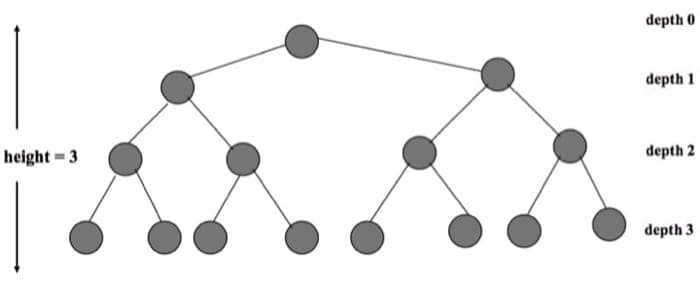
有根的树也是一棵 free tree，但是其中一个节点和其他不同，称为根。有根树中有一些概念需要理解清楚，这里只列举出来不再赘述：ancestor, descendant, proper ancestor, proper descendant, parent, child, siblings, external node(leaf), internal node。

一个节点的孩子数量称之为节点的度(degree)，从根到某节点的要经过的边的数量就是该节点的深度，最大的深度称为树的高度。

根树有几个特例，也非常常用，需要理解清楚，这里列举如下：

• Binary tree
• Full binary tree: each node is either a leaf or has degree exactly 2
• Complete k-ary tree: a k-ary tree in which all leaves have the same depth and all internal nodes have degree k
• Binary search tree: 一个节点的左右子节点和节点本身满足一定的大小关系

树的遍历

这一部分也是非常重要的内容，基本来说各类考点都在这里，不但需要对概念的清晰理解，还需要利用递归来解决问题（虽然不用递归也可以），主要有下面这四类：

1. 前序遍历
2. 中序遍历
3. 后序遍历
4. 层次遍历

具体的概念可以在 wiki 上查看，注意一下层次遍历可能需要一些特殊处理即可。

二叉树的常见操作包括树的遍历，即以一种特定的规律访问树中的所有节点。常见的遍历方式包括：

• 前序遍历(Pre-order traversal)：访问根结点；按前序遍历左子树；按前序遍历右子树。
• 中序遍历(In-order traversal)：按中序遍历左子树；访问根结点；按中序遍历右子树。特别地，对于二分查找树而言，中序遍历可以获得一个由小到大或者由大到小的有序序列。
• 后续遍历(Post-order traversal)：按后序遍历左子树；按后序遍历右子树；访问根结点。

以上三种遍历方式都是深度优先搜索算法(depth-first search)。深度优先算法最自然的实现方式是通过递归实现，事实上，大部分树相关的面试问题都可以优先考虑递归。此外，另一个值得注意的要点是：深度优先的算法往往都可以通过使用栈数据结构将递归化为非递归实现。这里利用了栈先进后出的特性，其数据的进出顺序与递归顺序一致(请见 Stack and Queue) 。

层次遍历(Level traversal)：首先访问第0层，也就是根结点所在的层；当第i层的所有结点访问完之后，再从左至右依次访问第i+1层的各个结点。层次遍历属于广度优先搜索算法(breadth-first search)。广度优先算法往往通过队列数据结构实现。

B-Tree

如果我们想要表示一个 complete binary tree 的话，其实可以用数组来完成，这种结构其实也可以看成是一个堆。堆的话需要理解的不算特别多，注意下最大堆最小堆，以及对应的操作即可。另外前面提到的优先队列也可以认为是堆，不过这个不展开了。

这一部分我们着重来看看 B-Tree，这是一类搜索树，在给定 n 个节点的条件下，尽可能减少树的高度，相对于原来的二叉搜索树，B-Tree 做了两个调整：

1. 节点可以有多于两个子节点
2. 节点中可以保存多个元素

因为需要保存不定数量的元素，所以一般用 set 来实现（这种情况下不允许有重复的元素，重复的情况这里暂时不考虑）。稍微提一下，许多数据库都是用 B-Tree 实现的。

所有的 B-Tree 都有一个非常重要的常数 MINIMUM，决定了每个节点中需要保存多少元素，具体的规则如下：

1. 根节点有 0 或 1 个元素，其他的节点至少需要保存 MINIMUM 个元素
2. 一个节点中最多可以保存 2*MINIMUM 个元素
3. 一个节点中保存的元素是有序的，从最小到最大
4. 假设一个非叶节点中存有 N 个元素，那么它会有 N+1 个子树
5. 对于任何一个非叶节点：
   • 第 I 个元素比其第 I 个子树的所有元素都要大
   • 第 I 个元素比其第 I+1 个子树的所有元素都要小
   • 
6. 每个叶节点都有相同的深度，也就是说 B-Tree 总是平衡的

下图是一个例子，其中 MINIMUM = 1，注意，根节点的每个子节点也是一颗 B-Tree

对应的数据结构是：

public class IntBalancedSet{
    // constants
    private static final MINIMUM = 200;
    private static final MAXIMUM = 2 * MINIMUM;
    // info about root node
    int dataCount;
    int[] data = new int[MAXIMUM + 1];
    int childCount;
    // info about children
    IntBalancedSet[] subset = new IntBalancedSet[MAXIMUM+2];
    // ....
}

例如：

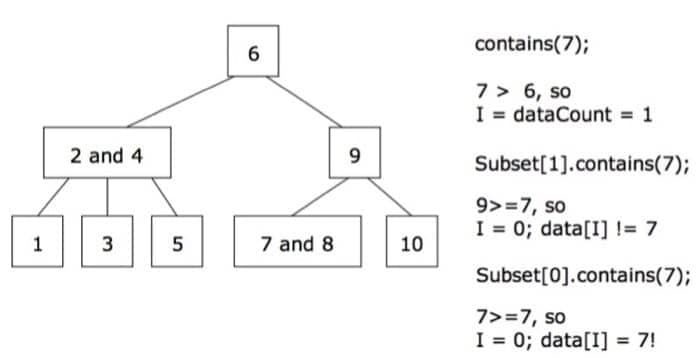
利用 B-Tree 进行搜索的方法如下：

• 找到这样一个 set，满足 data[I] >= target 且 I 尽可能小，如果找不到，则 I = dataCount
• 如果 data[I] == target 返回 true，如果不等于且没有子节点，返回 false
• 如果不等于但是有子节点，则返回 subset[I].contains(target)

一般来说，结构比较复杂的数据结构，进行修改都会比较麻烦（因为结构中内在的约束太多，变动的话需要满足所有约束），在 B-Tree 中添加和删除节点是比较复杂的操作。这里讲详细一些，用一个具体的例子来做说明（MINIMUM=1）

删除操作的伪代码：

Delete(T, X, success)
    // 从树 T 中删除 key 为 X 的节点，如果没有对应节点，则操作失败
    // 操作结果可以从 success 变量中获悉

    // 先找到 key 为 X 的节点的位置
    IF I is present THEN
        swap item I into leaf L which contains the inorder successor of I
        // 从 leaf L 开始删除操作
        IF L has no items THEN Fix(L)
        success := true
    ELSE
        success := false

然后是其中的 Fix 函数，用来处理没有子节点的节点，保证符合 B-Tree 的基本性质

Fix(N)
    // N 是一个没有子节点的节点
    // 如果 N 是一个 internal node，那么它有一个子节点

    Let P be the parent of N. If N is the root, delete it and return.

    IF some sibling of N has two items THEN
        distribute items among N, the sibling, and P

        IF N is internal THEN
            move the appropriate child from the sibling to N
    ELSE
        // 如果其兄弟没有两个子节点，就必须要进行融合
        Choose an adjancent sibling S of N

        Bring the appropriate item down from P into S

        IF N is internal THEN
            Move N's child to S

        Delete node N

        IF P is now without an item THEN Fix(P)

然后我们看看插入操作：

Insert(T, newitem)
    // 把 newitem 插入到树 T 中
    Let X be the search key of new item

    Locate the leaf L in which X belongs

    Add newitem to L

    IF L now has three items THEN
        Split(L)

继续来看看这里的 Split 函数

Split(N)
    // 分割那些有 3 个子节点的节点。注意如果 N 是 internal 的，它可以有 4 个孩子
    Let P be the parent of N
        // 如果 N 是根，那么创建一个新节点 P

    Replace node N by two nodes, N1 and N2

    Give N1 the item in N with the smallest search key value
    Give N2 the item in N with the largest search key value

    IF N is an iternal node THEN
        N1 becomes the parent of N's two leftmost children
        N2 becomes the parent of N's two rightmost children

    Send up to P the item in N with the middle search key value

    IF P now has 3 items THEN
        Split(P)

我们给定如下一颗 B-Tree

插入 39 之后（插入总是在叶节点）为

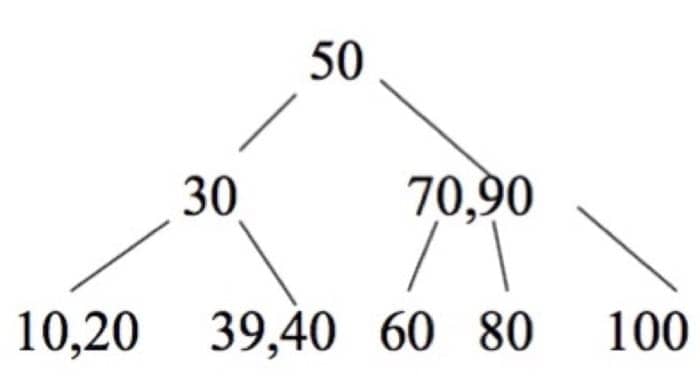
再插入 38，会发现有一个节点有多于 2 个子节点，需要 split

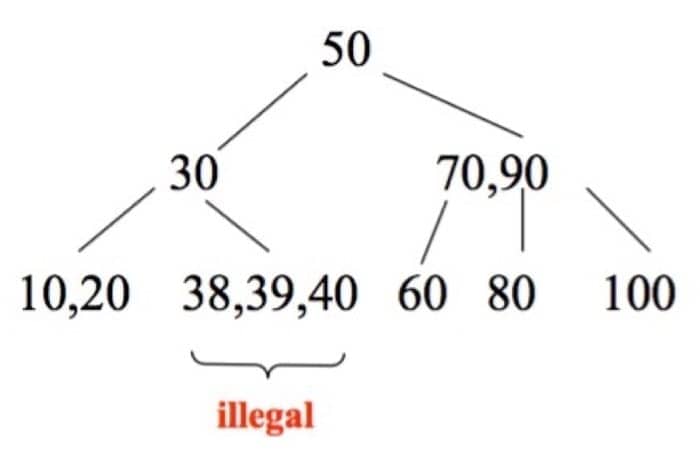
可以看到我们通过 split 操作把 39 提上去了（注意对照前面的 split 函数的伪代码来进行操作和理解）：

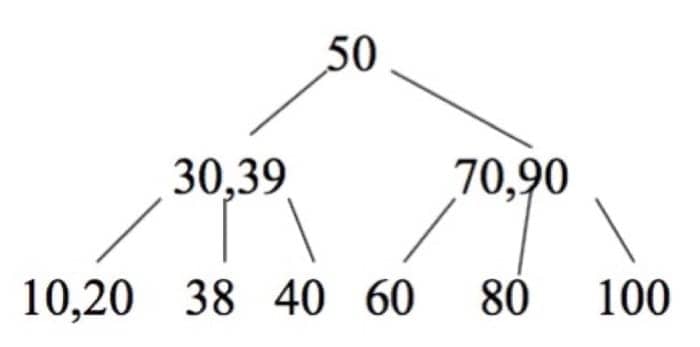
我们再插入 37 与 36，这会导致树高改变，需要进行更多操作，过程如下：

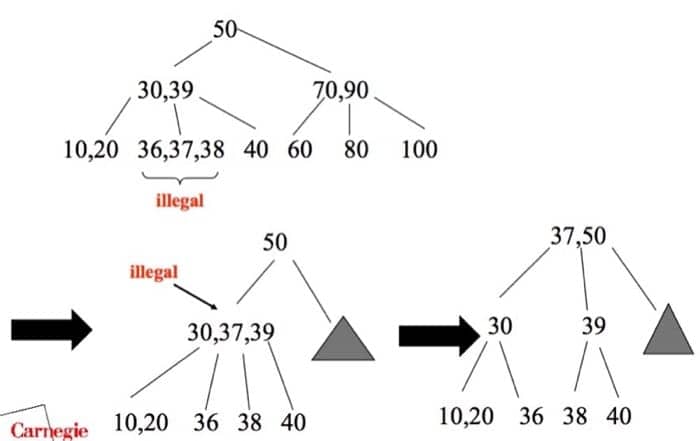
插入之后我们发现又出现了非法的节点，依照 split 规则更新之后，上层的节点再次非法，这里属于有四个子节点的情况，左右分开，把中间的 37 移上一层，就成为最后一个形态。

我们再多插入一些，比如 34，35，36，整个过程如下：

最后就得到

注意，因为向下传播的关系，高度是从顶层开始增长的。

然后我们来看看删除操作，还是用刚才的例子，给定：

这次我们删除 50，因为是根节点，所以需要找一个节点放到原来根的位置，并且需要把 70 下移以满足条件

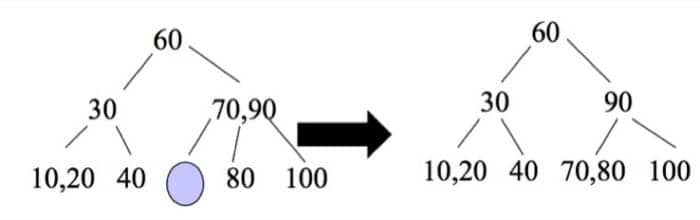
我们再删除 100 试试看：

同样对照前面的 Fix 函数进行操作即可。然后我们再删除 60，这里需要涉及的变动就会比较多，如下：

然后我们再删除 70 看看，就会变成这样：

最后再删除 80，又会进行一次融合

删除操作总是从 leaf 开始的，把要删除的节点和其 inorder successor 换位置。具体的操作如果还不明白，可以找一些视频来看看，这里不赘述了。

红黑树 Red Black Tree

这里只给出基本性质的说明，具体的细节可以查看这里

红黑树是每个节点都带有颜色属性的二叉查找树，颜色为红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求：

1. 节点是红色或黑色。
2. 根是黑色。
3. 所有叶子都是黑色（叶子是NIL节点）。
4. 每个红色节点必须有两个黑色的子节点。（从每个叶子到根的所有路径上不能有两个连续的红色节点。）
5. 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点。

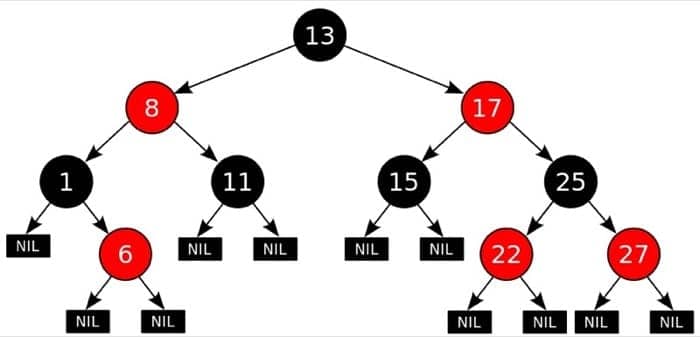
这些约束确保了红黑树的关键特性：从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

还是那句话对于约束较多的数据结构，进行插入和删除都是比较复杂的操作，最好通过例子掌握整个过程。

最后提一下复杂度，因为树的分叉设计，所以基本来说复杂度都是 log 的，但是需要注意，在最坏情况下，复杂度很可能是 O(n)。

Trie

字典树(trie or prefix tree)是一个26叉树，用于在一个集合中检索一个字符串，或者字符串前缀。字典树的每个节点有一个指针数组代表其所有子树，其本质上是一个哈希表，因为子树所在的位置(index)本身，就代表了节点对应的字母。节点与每个兄弟具有相同的前缀，这就是trie也被称为prefix tree的原因。

假设我们要存储如下名字，年龄：

Amy 12
Ann 18
Bob 30

则构成的字典树如下：

. root: level 0
a---------b level 1
| |
m---n o level 2
| | |
y n b level 3
| | |
12 18 30 level 4

由于Amy和Ann共享前缀a，故第二个字母m和n构成兄弟关系。

字典树以及字典树节点的原型：

class TrieNode {
    private:
        T mContent;
        vector<TrieNode*> mChildren;
    public:
        Node();
        ~Node();
        friend class Trie;
};
class Trie {
public:
    Trie();
    ~Trie();
    void addWord(string s);
    bool searchWord(string s);
    void deleteWord(string s);
private:
    TrieNode* root;
};

字典树的基本功能如下：

1) void addWord(string key, int value);

添加一个键:值对。添加时从根节点出发，如果在第i层找到了字符串的第i个字母，则沿该节点方向下降一层(注意，如果下一层存储的是数据，则视为没有找到)。否则，将第i个字母作为新的兄弟插入到第i层。将键插入完成后插入值节点。

2) bool searchWord(string key, int &value);

查找某个键是否存在，并返回值。从根节点出发，在第i层寻找字符串中第i个字母是否存在。如果是，沿着该节点方向下降一层；否则，返回false。

3) void deleteWord(string key)

删除一个键:值对。删除时从底层向上删除节点，“直到遇到第一个有兄弟的节点(说明该节点向上都是与其他节点共享的前缀)，删除该节点。

堆与优先队列

通常所说的堆(Heap)是指二叉堆，从结构上说是完全二叉树，从实现上说一般用数组。以数组的下标建立父子节点关系：对于下标为i的节点，其父节点为(int)i/2，其左子节点为2i，右子节点为2i+1。堆最重要的性质是，它满足部分有序(partial order)：最大(小)堆的父节点一定大于等于(小于等于)当前节点，且堆顶元素一定是当前所有元素的最大(小)值。

堆算法的核心在于插入，删除算法如何保持堆的性质(以下讨论均以最大堆为例):

下移(shift-down)操作：下移是堆算法的核心。对于最大值堆而言，对于某个节点的下移操作相当于比较当前节点与其左右子节点的相对大小。如果当前节点小于其子节点，则将当前节点与其左右子节点中较大的子节点对换，直至操作无法进行(即当前节点大于其左右子节点)。

建堆：假设堆数组长度为n，建堆过程如下，注意这里数组的下标是从 1 开始的：

for i, n/2 downto 1
    do shift-down(A,i)

插入：将新元素插入堆的末尾，并且与父节点进行比较，如果新节点的值大于父节点，则与之交换，即上移(shift-up)，直至操作无法进行。

弹出堆顶元素：弹出堆顶元素(假设记为A[1]，堆尾元素记为A[n])并维护堆性质的过程如下：

output = A[1]
exchange A[1] <-> A[n]
heap size -= 1
shift-down(A,1)
return output

值得注意的是，堆的插入操作逐层上移，耗时O(log(n))，与二叉搜索树的插入相同。但建堆通过下移所有非叶子节点(下标n/2至1)实现，耗时O(n)，小于BST的O(nlog(n))。

通过上述描述，不难发现堆其实就是一个优先队列。对于C++，标准模版库中的priority_queue是堆的一种具体实现。

图的表示

图(Graph)是节点集合的一个拓扑结构，节点之间通过边相连。图分为有向图和无向图。有向图的边具有指向性，即AB仅表示由A到B的路径，但并不意味着B可以连到A。与之对应地，无向图的每条边都表示一条双向路径。

图的数据表示方式也分为两种，即邻接表(adjacency list)和邻接矩阵(adjacency matrix)。对于节点A，A的邻接表将与A之间相连的所有节点以链表的形势存储起来，节点A为链表的头节点。这样，对于有V个节点的图而言，邻接表表示法包含V个链表。因此，链接表需要的空间复杂度为O(V+E)。邻接表适用于边数不多的稀疏图。但是，如果要确定图中边(u, v)是否存在，则只能在节点u对应的邻接表中以O(E)复杂度线性搜索。

对于有V个节点的图而言，邻接矩阵用V*V的二维矩阵形式表示一个图。矩阵中的元素Aij表示节点i到节点j之间是否直接有边相连。若有，则Aij数值为该边的权值，否则Aij数值为0。特别地，对于无向图，由于边的双向性，其邻接矩阵的转置矩阵为其本身。邻接矩阵的空间复杂度为O(V^2 )，适用于边较为密集的图。邻接矩阵在检索两个节点之间是否有边相连这样一个需求上，具有优势。

性能分析

这里主要看一下最坏情况

• 添加或删除边：
  • adjacency matrix: O(1)
  • edge list: O(N)
  • edge set: O(logN) - 使用 B-Tree
• 检查某条边是否存在：
  • adjacency matrix: O(1)
  • edge list: O(N)
  • edge set: O(logN) - 使用 B-Tree 或 红黑树
• 遍历某个节点的边：
  • adjacency matrix: O(N)
  • edge list: O(E) - 其中 E 是边的数目
  • edge set: O(E) - 使用 B-Tree 或 红黑树

图的遍历

对于图的遍历(Graph Transversal)类似于树的遍历(事实上，树可以看成是图的一个特例)，也分为广度优先搜索和深度优先搜索。算法描述如下：

广度优先

对于某个节点，广度优先会先访问其所有邻近节点，再访问其他节点。即，对于任意节点，算法首先发现距离为d的节点，当所有距离为d的节点都被访问后，算法才会访问距离为d+1的节点。广度优先算法将每个节点着色为白，灰或黑，白色表示未被发现，灰色表示被发现，黑色表示已访问。算法利用先进先出队列来管理所有灰色节点。一句话总结，广度优先算法先访问当前节点，一旦发现未被访问的邻近节点，推入队列，以待访问。

《算法导论》第22章图的基本算法给出了广度优先的伪代码实现，引用如下：

BFS(G, s)
For each vertex u exept s
    Do Color[u] = WHITE
        Distance[u] = MAX
        Parent[u] = NIL
Color[s] = GRAY
Distance[s] = 0
Parent[s] = NIL
Enqueue(Q, s)
While Q not empty
    Do u = Dequeue(Q)
        For each v is the neighbor of u
            Do if Color[v] == WHITE
                Color[v] = GRAY
                Distance[v] = Distance[u] + 1
                Parent[v] = u
                Enqueue(Q, v)
            Color[u] = BLACK”

深度优先

深度优先算法尽可能“深”地搜索一个图。对于某个节点v，如果它有未搜索的边，则沿着这条边继续搜索下去，直到该路径无法发现新的节点，回溯回节点v，继续搜索它的下一条边。深度优先算法也通过着色标记节点，白色表示未被发现，灰色表示被发现，黑色表示已访问。算法通过递归实现先进后出。一句话总结，深度优先算法一旦发现没被访问过的邻近节点，则立刻递归访问它，直到所有邻近节点都被访问过了，最后访问自己。

《算法导论》第22章图的基本算法给出了深度优先的伪代码实现，引用如下：

DFS(G)
For each vertex v in G
    Do Color[v] = WHITE
    Parent[v] = NIL
For each vertex v in G
    DFS_Visit(v)

DFS_Visit(u)
Color[u] = GRAY
For each v is the neighbor of u
    If Color[v] == WHITE
        Parent[v] = u
        DFS_Visit(v)
Color[u] = BLACK

图的实现

public class Graph {
    private boolean[][] edges;
    private Object[] labels;

    public Graph (int n){
        edges = new boolean[n][n];
        labels = new Object[n];
    }

    public void addEdge (int s, int t) {
        edges[s][t] = true;
    }

    public Object getLabel(int v) {
        return labels[v];
    }

    public boolean isEdge(int s, int t) {
        return edges[s][t];
    }

    public int[] neighbors(int v) {
        int i;
        int count;
        int[] answer;
        count = 0;
        for (i = 0; i < labels.length; i++{
            if (edges[v][i]) count++;
        }
        answer = new int[count];
        count = 0;
        for (i = 0; i < labels.length; i++) {
            if (edges[v][i]) answer[count++] = i;
        }
        return answer;
    }

    public void removeEdge(int s, int t) {
        edges[s][t] = false;
    }

    public void setLabel(int v, Object n){
        labels[v] = n;
    }

    public int size() {
        return labels.length;
    }
}

解题策略

对于树和图的性质，一般全局解依赖于局部解。通常可以用DFS来判断子问题的解，然后综合得到当前的全局结论。

值得注意的是，当我们在传递节点指针的时候，其实其代表的不只是这个节点本身，而是指对整个子树、子图进行操作。只要每次递归的操作对象的结构一致，我们就可以选择Divide and Conquer(事实上对于树和图总是如此，因为subgraph和subtree仍然是graph和tree结构)。实现函数递归的步骤是：首先设置函数出口，就此类问题而言，递归出口往往是node == NULL。其次，在构造递归的时候，不妨将递归调用自身的部分视为黑盒，并想象它能够完整解决子问题。以二叉树的中序遍历为例，函数的实现为：

void InOrderTraversal(TreeNode *root) {
    if (root == NULL) {
        return;
    }
    InOrderTraversal(root->left);
    root->print();
    InOrderTraversal(root->right);
}

想象递归调用的部分 InOrderTraversal(root->left)／InOrderTraversal(root->right)能够完整地中序遍历一棵子树，那么根据中序遍历“按中序遍历左子树；访问根结点；按中序遍历右子树”的定义，写出上述实现就显得很自然了。

DFS 处理树的问题

有一类关于树的问题是， 要求找出一条满足特定条件的路径 。对于这类问题，通常都是传入一个 vector 记录当前走过的路径(为尽可能模版化，统一记为path)，传入 path 的时候可以是引用，可以是值。还需要传入另一个 vector 引用记录所有符合条件的 path (为尽可能模版化，统一记为result)。注意， result 可以用引用或指针形式，相当于一个全局变量，或者就开辟一个独立于函数的成员变量。由于 path 通常是vector ，那么result就是 。当然，那个特定条件，也是函数的一个输入变量。

在解答此类问题的时候，通常都采用DFS来访问，利用回溯思想，直到无法继续访问再返回。值得注意的是，如果path本身是以引用(reference)的形式传入，那么需要在返回之前消除之前所做的影响(回溯)。因为传引用(Pass by reference)相当于把path也看作全局变量，对path的任何操作都会影响其他递归状态，而传值(pass by value)则不会。传引用的好处是可以减小空间开销。

树和其他数据结构的相互转换

这类题目要求将树的结构转化成其他数据结构，例如链表、数组等，或者反之，从数组等结构构成一棵树。前者通常是通过树的遍历，合并局部解来得到全局解，而后者则可以利用D&C的策略，递归将数据结构的两部分分别转换成子树，再合并。

寻找特定节点

此类题目通常会传入一个当前节点，要求找到与此节点具有一定关系的特定节点：例如前驱、后继、左／右兄弟等。

对于这类题目，首先可以了解一下常见特定节点的定义及性质。在存在指向父节点指针的情况下，通常可以由当前节点出发，向上倒推解决。如果节点没有父节点指针，一般需要从根节点出发向下搜索，搜索的过程就是DFS。

图的访问

关于图的问题一般有两类。一类是前面提到的关于图的基本问题，例如图的遍历、最短路径、可达性等；另一类是将问题转化成图，再通过图的遍历解决问题。第二类问题有一定的难度，但也有一些规律可循：如果题目有一个起始点和一个终止点，可以考虑看成图的最短路径问题。

单源最短路径问题

对于每条边都有一个权值的图来说，单源最短路径问题是指从某个节点出发，到其他节点的最短距离。该问题的常见算法有Bellman-Ford和Dijkstra算法。前者适用于一般情况(包括存在负权值的情况，但不存在从源点可达的负权值回路)，后者仅适用于均为非负权值边的情况。Dijkstra的运行时间可以小于Bellman-Ford。本小节重点介绍Dijkstra算法。

特别地，如果每条边权值相同(无权图)，由于从源开始访问图遇到节点的最小深度 就等于到该节点的最短路径，因此 Priority Queue就退化成Queue，Dijkstra算法就退化成BFS。

Dijkstra的核心在于，构造一个节点集合S，对于S中的每一个节点，源点到该节点的最短距离已经确定。进一步地，对于不在S中的节点，“我们总是选择其中到源点最近的节点，将它加入S，并且更新其邻近节点到源点的距离。算法实现时需要依赖优先队列。一句话总结，Dijkstra算法利用贪心的思想，在剩下的节点中选取离源点最近的那个加入集合，并且更新其邻近节点到源点的距离，直至所有节点都被加入集合。关于Dijkstra算法的正确性分析，可以使用数学归纳法证明，详见《算法导论》第24章，单源最短路径。 给出伪代码如下：

DIJKSTRA(G, s)
S = EMPTY
Insert all vertexes into Q
While Q is not empty
    u = Q.top
    S.insert(u)
    For each v is the neighbor of u
        If d[v] > d[u] + weight(u, v)
            d[v] = d[u] + weight(u, v)
            parent[v] = u

任意两点之间的最短距离

另一个关于图常见的算法是，如何获得任意两点之间的最短距离(All-pairs shortest paths)。直观的想法是，可以对于每个节点运行Dijkstra算法，该方法可行，但更适合的算法是Floyd-Warshall算法。

Floyd算法的核心是动态编程，利用二维矩阵存储i，j之间的最短距离，矩阵的初始值为i，j之间的权值，如果i，j不直接相连，则值为正无穷。动态编程的递归式为：d(k)ij = min(d(k-1)ij, d(k-1)ik+ d(k-1)kj) (1<= k <= n)。直观上理解，对于第k次更新，我们比较从i到j只经过节点编号小于k的中间节点(d(k-1)ij)，和从i到k，从k到j的距离之和(d(k-1)ik+ d(k-1)kj)。Floyd算法的复杂度是O(n^3)。关于Floyd算法的理论分析，请见《算法导论》第25章，每对顶点间的最短路径。 给出伪代码如下：

FLOYD(G)
Distance(0) = Weight(G)
For k = 1 to n
    For i = 1 to n
        For j = 1 to n
Distance(k)ij = min(Distance (k-1)ij, Distance (k-1)ik+ Distance(k-1)kj)
Return Distance(n)

附录

• Zigzag Level Order Traversal
• Word Ladder
• Word Ladder II
• Valid Binary Search Tree
• Unique Binary Search Trees
• Unique Binary Search Trees II
• Implement Trie (Prefix Tree)
• Topological Sort
• Convert Sorted List to Binary Search Tree
• Sorted Array to Binary Search Tree
• Serialize and Deserialize
• Search Range
• Scramble String
• Route Between Nodes
• Root Path Sum
• Binary Tree Right Side View
• Reverse Binary Tree
• Recover Binary Search Tree
• Preorder Traversal
• Postorder Traversal
• Node Path Sum
• Paths with Sum II
• Populating Next Right Pointers in Each Node
• Next Node without Parent
• Next Node
• Next Node in BST
• Neighbor Node
• Minimum Path Sum
• Min Height of Binary Tree
• Min Height of Binary Tree
• Maximum Path Sum
• Height of Binary Tree
• Level Order Traversal
• Level Order Traversal II
• Leaf Path Sum
• Kth Smallest Element in a BST
• Is Subtree
• Insert node to BST
• Inorder Traversal
• Flatten Binary Tree to Linked List
• First Common Ancestor
• First Common Ancestor of a Binary Search Tree
• Different BST
• Different BST II
• Course Schedule
• Course Schedule II
• Connected Nodes in Undirected Graph
• Complete Tree Node Count
• Clone Graph
• Symmetric Tree
• Same Tree
• Build Order
• BST Sequences
• Binary Tree to Linked List
• Construct Binary Tree from Preorder and Inorder Traversal
• Construct Binary Tree from Inorder and Postorder Traversal
• Binary Tree Depth
• Binary Search Tree Iterator
• Balance Tree
• Balance Tree
• All Path