【编程起跑线】02 Big O 分析

前一讲大概了解了这个系列会涉及的内容，这一讲就从最重要的概念，Big O 开始讲起。既然我们要找到效率更高的算法，首先就得知道，怎么样才是高效率。

更新历史

2019.08.05：编入新系列
2016.01.22：完成初稿

前条件/后条件

建议在写具体的函数之前，都要先想好（写好）前条件和后条件，这样可以确定问题的边界。

前条件：在函数调用之前一定为真的条件
后条件：在函数执行完之后为真的条件

例如：

// Precondition: x >= 0
// Postcondition: The square root of x has
// been written to the standard output
public void writeSqrt(double x){
...
}

Big O

在具体介绍之前，先来一些基本的数学公式复习

$log_b(x_1·x_2)=log_bx_1+log_bx_2$

$log_b(\frac{x_1}{x_2})=log_bx_1-log_bx_2$

$log_b(x^c)=c·log_bx$

事实上除了我们常用的 Big O，还有另外两种表示的方法：Big Omega( $Big- \Omega$ ) 和 Big Theta( $Big - \theta$ )

这里只介绍它们的差别，具体的定义可以自行查看。

Big-O 实际上只表示上限，比如说，我们知道 $17n^2\in O(n^2)$ ，但是同时我们也可以说 $17n^2\in O(n^37)$ 和 $17n^2\in O(2^n)$

Big omega 则是表示下限，例如 $f(n) = n$ ，那么下面两个式子都成立 $f(n) \in O(n^2)$ 与 $n^2 \in \Omega(n)$

而 Big theta(Big $\theta$ ) 则是前面两个的交集：

$\theta(f)=O(f) \cap \Omega(f)$

举例来说，函数 $f(n) = 4n$ ，则

$f(n)\in O(n)$

$f(n) \in \Omega(n)$

所以

$f(n)\in \theta(n)$

简单来说就是

Big O 是一个算法最坏情况的度量
Big Omega 是一个算法最好情况的度量
Big Theta 表达了一个算法的区间，给定了一个函数的渐近的逼近(asymptotically tight bound)

但是一般来说用 Big O 也就足够了

基本法则

我们先来了解一下程序分析的基本法则。一般来说，常见的输入输出以及简单的赋值语句，可以认为时间复杂度是 O(1)。在算复杂度的时候乘以一个常数复杂度不变，即 $O(Cf(n)) = O(f(n))$ ，其中C是一个正常数。

我们知道，程序设计中无非是三种形态：顺序，选择和循环，只要能够算清楚这三种形态的复杂度，那么整个算法的复杂度也就不在话下了。

先来看看顺序结构，因为是顺序执行，所以可以通过求和法则来进行计算。若算法的 2 个部分时间复杂度分别为 $T1(n)=O(f(n))$ 和 $T2(n)=O(g(n))$ ,则 $T1(n)+T2(n)=O(max(f(n), g(n)))$ 。如果这两个部分的参数不一样的话，即 $T1(m)=O(f(m))$ 和 $T2(n)=O(g(n))$ ,则 $T1(m)+T2(n)=O(f(m) + g(n))$

然后是选择结构，选择本身判断是耗费 O(1) 时间的，但是主要时间还是在执行不同的子句上，所以转换为分析子句的时间复杂度。

最后来看看循环结构，一般来说可能包括多次循环，所以使用乘法法则。若算法的2个部分时间复杂度分别为 $T1(n)=O(f(n))$ 和 $T2(n)=O(g(n))$ ,则 $T1 \times T2=O(f(n) \times g(n))$ 。

基本上理解了什么时候用求和法则，什么时候用乘法法则，再加上一点点运算，就可以推算出时间复杂度了。

递归

递归问题应该算是求复杂度问题中比较麻烦的了，并不像其他非递归的算法可以用上面提到的基本法则来进行分析。一般来说，遇到递归问题，有两种做法：

主定理法
递归树法

实际上主定理法可以看作是递归树法的一个总结，这里用一个例子来说明，假设我们的递归函数是： $T(n) = T(\frac{n}{3}) + T(\frac{2n}{3}) + n$ ，那么画出递归树就是：

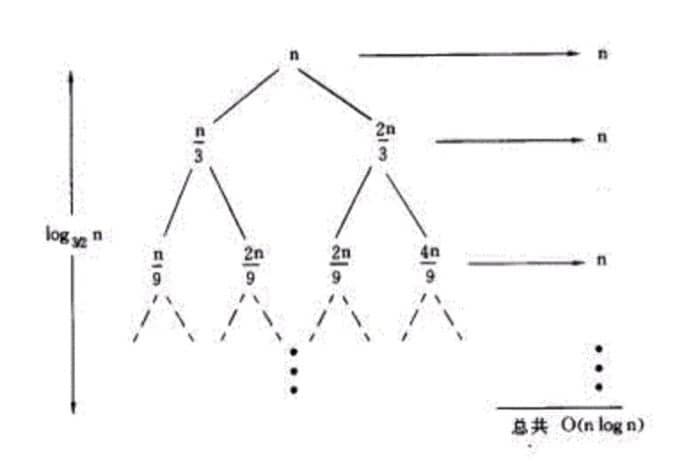
每层都会多出来一个 n，而从根到叶节点的最长路径是： $n \to \frac{2}{3}n \to (\frac{2}{3})^2n \to \dots \to 1$ ，假设一共有 k 层，因为 $(\frac{2}{3})^kn = 1$ ，所以 $k=log_{3/2}n$ ，也就是说 $T(n) \le \sum_{i=0}^k n = (k+1)n = n(log_{3/2}n+1 )$ ，即 $T(n) = O(nlog\;n)$

我们来看看用主定理方法的话，这个复杂度要怎么算。首先我们要把递推公式转换为如下形式：

$f(n)=af(\frac{n}{b}) + d(n)$

然后分情况进行讨论：

而这题中 $T(n) = T(\frac{n}{3}) + T(\frac{2n}{3}) + n$ ，化简之后相当于 $a=3,b=3$ ，于是在第二种情况中找到 $a=b$ 的情况，就得到了最后的结果 $O(nlog\; n)$

例题

这里主要是提及一些容易出错的地方。

不是出现了树结构，就一定会产生 log 的复杂度

假设代码如下：

int sum(Node node){
    if (node == null){
        return 0;
    }
    return sum(node.left) + node.value + sum(node.right);
}

因为实际上是遍历所有的节点一次，于是复杂度是 O(n)

有的时候可以通过这个代码的做用来进行复杂度判断

来看看下面这两个代码片段：

// 片段 1
boolean isPrime(int n){
    for (int x = 2; x * x <= n; x++){
        if (n % x == 0){
            return false;
        }
    }
    return true;
}


// 片段 2
void permuation(String str){
    permutation(str, "");
}
void permutation(String str, String prefix){
    if (str.length() == 0){
        System.out.println(prefix);
    }
    else {
        for (int i = 0; i < str.length(); i++){
            String rem = str.substring(0,i) + str.substring(i+1);
            permutation(rem, prefix + str.charAt(i));
        }
    }
}

第一题比较简单，因为是求质数，在 $\sqrt n$ 时间就可以完成，对应的时间复杂也就是出来了。

第二题做得是一个全排列，可以从两个思路：What It Means 和 What It Does。

What It Means：因为是求排列，如果一个字符串有n个字符，那么所有的可能为 n*(n-1)*...*2*1 -> O(n!)
What It Does：设一共有 n 个字符，第一次循环，有 n 次递归调用，第二次有 n-1 次，到最后一共有 n*(n-1)*...*2*1 -> O(n!)

最后再举一个递归的例子

int fib(int n){
    if (n <= 0) return 0;
    else if (n == 1) return 1;
    return fib(n-1) + fib(n-2);
}

这里每一次递归，都会由原来的一个分成两个，而一共有 n 层，于是时间复杂度为 $O(2^N)$

总结

当然，很多时候还需要具体问题具体分析，最关键的，是对算法过程的清晰理解和掌握，有了这个，哪怕从头开始一点一点分析，也可以推导出正确答案。