Published on

【论文笔记】002 Optimal RealTime Bidding for Display Advertising

本文把程序化竞价当做是一个函数优化问题，其他特点：

  • optimal bid 与 impression level 特征（如点击率和转化率）存在非线性关系（之前的研究大多基于线性关系）
  • 更应该去竞价得到更多的展示，而不是只专注于少量高价值的展示，这样成本更低，也更容易竞价成功

更新历史

  • 2019.05.05: 完成初稿

摘要

  • RTB 与基于上下文的广告不同点在于更加关注用户数据，根据用户本身决定是否投放广告
  • RTB 与搜索引擎竞价广告的不同在于搜索引擎广告的价格是跟关键词绑定的，RTB 则是动态的
  • RTB 关键技术是基于预算和用户的各类信息自动进行竞价

本文把程序化竞价当做是一个函数优化问题，其他特点：

  • optimal bid 与 impression level 特征（如点击率和转化率）存在非线性关系（之前的研究大多基于线性关系）
  • 更应该去竞价得到更多的展示，而不是只专注于少量高价值的展示，这样成本更低，也更容易竞价成功

1 介绍

  • RTB 与基于上下文的广告以及搜索引擎关键词广告都不同
  • DSP 因此应运而生帮助广告主来进行竞价
  • 关于 RTB 更详细的介绍可以查看
    • Real-time bidding: A new frontier of computational advertising research [35]
    • Real-time bidding for onling advertising: measurement and analysis [38]

收到 Bid Request 之后 DSP 会选出所有符合广告位等要求的创意，然后分别计算出竞价价格。这里会使用上下文信息（域名、网页、关键词、时间、地理位置、天气、语言、操作系统、浏览器等等）以及行为信息（搜索、浏览、购买历史、收入、情感等等）进行计算。这是 DSP 最需要解决的问题，解决这个问题的方法称为 bidding strategy(竞价策略)

在纯粹的次高价投标(second price auctions)中，对于广告主来说的策略很简单：按照 private value 出价。什么是 private value，就是根据一次展示的 CTR/CVR 乘以一次点击/转换的价值（这样可以保证不亏本），很多广告主就计算这样一个值，然后一直使用。

但其实还有很多其他的信息需要考虑，比如 bid landscape(出价效果概况，可以估算广告组、条件和广告系列在不同出价情形下的效果。然后便可依据这些信息调整和优化出价策略)、总预算以及 campaign 剩余时长（比如这次计划投放三个月，现在已经过去了两个月）

本文实际上提出的就是一个把独立展示映射到竞价价格的函数(a function that maps the individual imporession evaluation to the bid value)。整个框架还包括：

  • 给定的预算限制和整个投放的时长
  • 考虑各类数据包括：竞价成功率、先验 impression feature 的分布

结果表明：

  • winning function 是一个非线性凹函数
  • 多投 higher bids for impressions with low estimated value，因为更便宜并且获胜率更高

2 相关工作

  • 在线广告中竞价优化是一个研究比较透彻的问题，但是主要集中在关键词竞价领域
  • 预算优化问题：给定总预算，优化广告效果

总而言之就是前面的竞价优化都不是针对 RTB 的都不能用，所以我们这个工作有用

  • Pacing problem：[25]

3 最优实时竞价

标记说明：

  • x\boldsymbol{x}：通过 feature 表示的 bid request
  • px(x)p_x(\boldsymbol{x})：x 的概率密度函数
  • θ(x)\theta(\boldsymbol{x})：如果赢得 x 的竞价对应的 KPI，可以是 CTR/CVR 等等
  • pθ(θ)p_\theta(\theta)：KPI θ\theta 的概率密度函数
  • NTN_T：在整个投放时长 T 中预计的 bid request 个数
  • b(θ(x),x)b(\theta(\boldsymbol{x}),\boldsymbol{x})：定义为一个函数的 bidding strategy，假设生成顺序 x→θ→b\boldsymbol{x} \to \theta \to b，那么可以记为 b(θ(x))b(\theta(\boldsymbol{x}))
  • w(b(θ(x)),x)w(b(\theta(\boldsymbol{x})),\boldsymbol{x})：对于给定的 bid request x\boldsymbol{x} 和 bid price b(θ(x))b(\theta(\boldsymbol{x})) 可能的获胜概率。假设生成顺序 x→θ→b→w\boldsymbol{x} \to \theta \to b \to w，那么可以记为 w(b(θ(x)))w(b(\theta(\boldsymbol{x})))

3.1 问题定义

为了开始一次广告投放，广告主会先上传创意，设定定向规则（人群、时间、地点），设定预算以及投放时长。设定好规则之后会先花一小部分的预算进行随机投放，以便收集一些数据。结合前面的标记，我们的优化目标为：

b()ORTB=argmaxb()NT∫xθ(x)w(b(θ(x),x),x)px(x)dxb()_{ORTB}= \underset{b()}{\mathrm{argmax}} N_T\int_x\theta(\boldsymbol{x})w(b(\theta(\boldsymbol{x}),\boldsymbol{x}),\boldsymbol{x})p_x(\boldsymbol{x})d\boldsymbol{x}

约束条件为：

NT∫xb(θ(x),x)w(b(θ(x),x),x)px(x)dx≤BN_T\int_xb(\theta(\boldsymbol{x}),\boldsymbol{x})w(b(\theta(\boldsymbol{x}),\boldsymbol{x}),\boldsymbol{x})p_x(\boldsymbol{x})d\boldsymbol{x} \le B

  • ORTB = Optimal Real-Time Bidding
  • θ(x)\theta(\boldsymbol{x}) 和 w(b,x)w(b,\boldsymbol{x}) 的乘积表示给定一个展示竞价的点击概率（这里用点击作为 KPI）
  • RTB 一般用次高价作为价格，但是因为 reserve price（保留价）的存在，一般来说价格会高于 second price，所以这里用 bid price b(θ(x),x)b(\theta(\boldsymbol{x}), \boldsymbol{x}) 作为获胜价格的上界
  • b(θ(x),x)b(\theta(\boldsymbol{x}), \boldsymbol{x}) 与获胜率的乘积是每次竞价的期望成本，再乘以 NTN_T 就是期望成本

这整个过程可以看做是一个 POMDPs(partially observable Markov decision processes)，但这计算量太大，所以转为用一个两步的方法：学习统计数据（如px(x)p_x(\boldsymbol{x})，和 NTN_T），然后优化竞价。我们假设统计模型满足如下的分布：每个特征向量（即每个 bid request）独立地由一个相同的分布产生。

为了让问题可解，我们认为变量有如下的序列依赖：

  • 假设 b(θ(x),x)≡b(θ(x))b(\theta(\boldsymbol{x}), \boldsymbol{x})\equiv b(\theta(\boldsymbol{x}))，即 bid 只取决于 CTR
  • 假设 w(b,x)≡w(b)w(b,\boldsymbol{x})\equiv w(b)，即特征 x 只通过影响 bid 来影响或胜率

那么前面的公式可以重写为

b()ORTB=argmaxb()NT∫xθ(x)w(b(θ(x)))px(x)dxb()_{ORTB}= \underset{b()}{\mathrm{argmax}} N_T\int_x\theta(\boldsymbol{x})w(b(\theta(\boldsymbol{x})))p_x(\boldsymbol{x})d\boldsymbol{x}

约束条件为：

NT∫xb(θ(x))w(b(θ(x)))px(x)dx≤BN_T\int_xb(\theta(\boldsymbol{x}))w(b(\theta(\boldsymbol{x}))) p_x(\boldsymbol{x})d\boldsymbol{x} \le B

更进一步，因为 x\boldsymbol{x} 和 θ(x)\theta(\boldsymbol{x}) 有一个确定的关系，所以可以做如下的转换：

pθ(θ(x))=px(x)∣∣∇θ(x)∣∣p_\theta(\theta(\boldsymbol{x}))=\frac{p_x(\boldsymbol{x})}{||\nabla\theta(\boldsymbol{x})||}

也就是说可以把 px(x)p_x(\boldsymbol{x}) 给替换成 θ\theta，即可以理解为赢得竞价之后，用户的点击率（这里我们优化点击），最终的公式为：

b()ORTB=argmaxb()NT∫θθw(b(θ))pθ(θ)dθb()_{ORTB}= \underset{b()}{\mathrm{argmax}} N_T\int_\theta\theta w(b(\theta))p_\theta(\theta)d\theta

约束条件为：

NT∫θb(θ)w(b(θ))pθ(θ)dθ≤BN_T\int_\theta b(\theta)w(b(\theta)) p_\theta(\theta)d\theta \le B

3.2 最优解

TODO 这里需要学习

用 Lagrangian 优化法进行求解，会发现 KPI 概率密度函数 pθ(θ)p_\theta(\theta) 会被消掉，bidding function b(θ)b(\theta)（就是确定最终出价的函数）只跟 winning function w(b(θ))w(b(\theta)) 有关。不同的 winning function 会得出不同的最优 bidding function。

Lagrangian 法得到的最终公式为（公式 1）：

λw(b(θ))=[θ−λb(θ)]∂w(b(θ))∂b(θ)\lambda w(b(\theta))=[\theta-\lambda b(\theta)]\frac{\partial w(b(\theta))}{\partial b(\theta)}

Winning & Bidding Function 1

经过试验得知，获胜率 w(b)w(b) 是一个凹函数：在竞价比较低的时候，加上一个单位价格对获胜率的影响要比在竞价高的时候大，可得 winning function 为（这个就满足随着 b 变大，w 增长越来越慢的规律，因为我们需要去求解，所以需要一个凸函数）

w(b(θ))=b(θ)c+b(θ)w(b(\theta))=\frac{b(\theta)}{c+b(\theta)}

其中 c 是一个常量，我们对 b 求微分可得

∂w(b(θ))∂b(θ)=c(c+b(θ))2\frac{\partial w(b(\theta))}{\partial b(\theta)}=\frac{c}{(c+b(\theta))^2 }

把前面俩公式带入到公式 1 中可得：

θc(c+b(θ))2−λ[b(θ)c+b(θ)+cb(θ)(c+b(θ))2]=0\frac{\theta c}{(c+b(\theta))^2}-\lambda\left[\frac{b(\theta)}{c+b(\theta)} + c\frac{b(\theta)}{(c+b(\theta))^2}\right] = 0

化简一下可得：

(b(θ)+c)2=c2+θcλ(b(\theta)+c)^2=c^2 + \frac{\theta c}{\lambda}

求解可得一个凹函数：

bORTB1(θ)=cλθ+c2−cb_{ORTB1}(\theta)=\sqrt{\frac{c}{\lambda}\theta+c^2} -c

Winning & Bidding Function 2

在某些情况下，因为有保留价的存在，所以在 bid price 很低的时候获胜率并不会随着竞价上升而快速增长，只有在竞价大于某个非零值得时候才会快速增长（在 high-profile ad slots 上常见），为了拟合这样的情况，我们微调 winning function：

w(b(θ))=b2(θ)c2+b2(θ)w(b(\theta))=\frac{b^2(\theta)}{c^2+b^2(\theta)}

同样的方式求解可得一个凹函数：

c⋅[(θ+c2λ2+θ2cλ)13−(cλθ+c2λ2+θ2)13]c\cdot\left[\left(\frac{\theta+\sqrt{c^2\lambda^2+\theta^2}}{c\lambda}\right)^{\frac{1}{3}}-\left(\frac{c\lambda}{\theta+\sqrt{c^2\lambda^2 + \theta^2 }}\right)^{\frac{1}{3}}\right]

Optimal Solution of λ\lambda

本文的方法会更多的把钱花在竞价较低的广告位上。我们最后来看看 λ\lambda 的值如何确定，还是拉格朗日乘子法，可得：

∫θb(θ,λ)w(b(θ,λ))pθ(θ)dθ=BNT\int_\theta b(\theta, \lambda)w(b(\theta,\lambda))p_\theta(\theta)d\theta=\frac{B}{N_T}

在很多情况下是没有可以通过解方程找到最优解的可能的，我们需要通过迭代法找到最优值。观察方程可得：B/NTB/N_T 越大，λ\lambda 就越小，也就意味着更高的竞价

4 试验设置

  • 包含离线和在线试验
  • train/test 比例为 2：1，按照时间序列切分，训练数据主要用来训练 CTR 预估器

5 离线评估

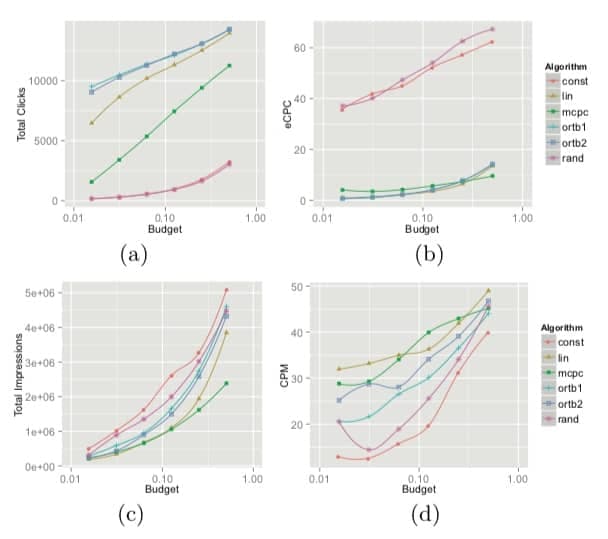
  • 比原来的线性模型有比较稳定的提高，在预算低的时候提高尤其明显（在这种情况下普通的线性模型会快速消耗预算，而本文的方法会更多在低价格 bid 尝试）
  • 预算增加的情况下点击数目和 eCPC 都会有增长
  • 可以看到 orbt1/2 在获得最多点击的条件下，总展示 impressions 次数也处于中游，对广告主比较有利（有种自卖自夸的感觉2333）
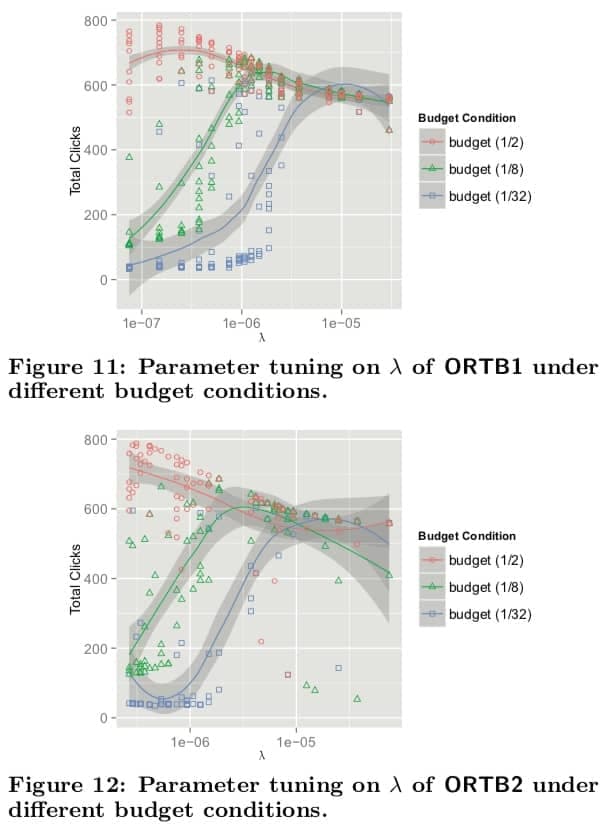
  • λ\lambda 的值可以直接计算得出，这里用试验的形式来进行测试
  • 可以看到预算越少，λ\lambda 的最优取值就越大

6 在线测试

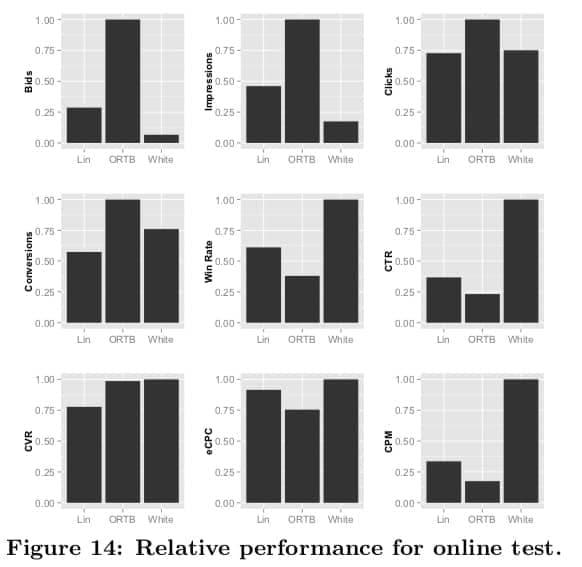
ORTB 对比其他拿到了最多的展示、点击和转化，以及最低的 eCPC

7 总结与未来工作

总结简单来说就是一句话：这个方法比以前的好，理论、离线和在线都验证过，怎么说，666

那么如何用在我们的代码里，很简单，关注下面这俩公式：

bORTB1(θ)=cλθ+c2−cb_{ORTB1}(\theta)=\sqrt{\frac{c}{\lambda}\theta+c^2} -c

和

c⋅[(θ+c2λ2+θ2cλ)13−(cλθ+c2λ2+θ2)13]c\cdot\left[\left(\frac{\theta+\sqrt{c^2\lambda^2+\theta^2}}{c\lambda}\right)^{\frac{1}{3}}-\left(\frac{c\lambda}{\theta+\sqrt{c^2\lambda^2 + \theta^2 }}\right)^{\frac{1}{3}}\right]

这里的变量就仨：θ,λ,c\theta,\lambda,c

  • c 是一个常数，可以根据需要的曲线设置，或者边尝试边设置，或通过历史竞价成功率进行拟合求解
  • θ\theta 就是预估的点击率，这个是由另一个算法得出，这个环节不操心
  • λ\lambda 是拉格朗日乘子，这个参数同样需要进行边尝试边设置，通过历史日志数据进行调整

总结起来就是出价的函数把上面俩公式翻译出来，然后具体的值进行测试确定即可。

未来方向：让 bidding function 直接包含 bid request feature，而不是只包含 KPI（也就是 θ\theta）

其他