前面我们了解了加速模型训练的技巧,这节课我们来看看更为关键的优化算法。
更新历史
- 2019.10.16: 完成初稿
Mini-batch 梯度下降
使用 batch 梯度下降法,一次遍历训练集 = 一次梯度下降优化,在训练集非常大的时候,速度会非常慢。但是如果使用 mini-batch 的话,一次遍历可以下降很多次,可以更快得到比较好的参数组合。对比如下图所示:
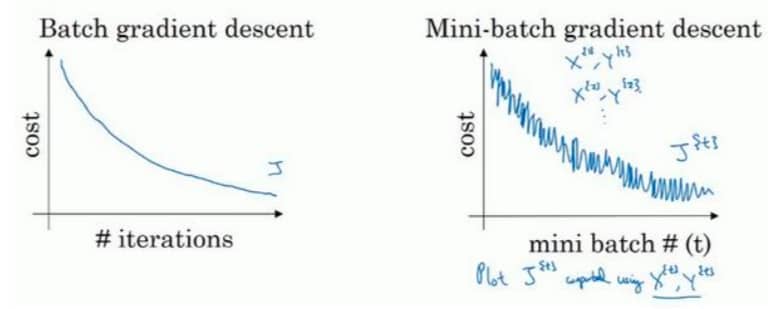
对于 batch 梯度下降法来说,每次迭代后,成本函数 J 一定会下降。但是对于 mini-batch 来说,成本函数是波动向下的。当 mini-batch 小到极致,就是只有一个样本的时候,就变成了随机梯度下降法(sgd)。随机梯度下降(紫色)、mini-batch(绿色)与 batch(蓝色)的对比如下图所示:
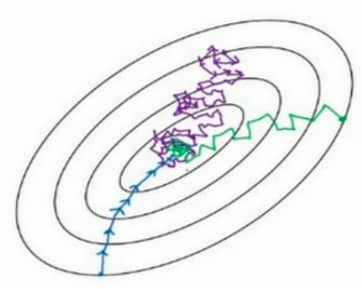
在实际使用时,我们一般会选择采用 mini-batch,那么问题来了,每个 mini-batch 中的样本数 m 要如何确定?
- 如果训练集较小(2000 个以下),直接 batch 梯度下降
- 如果训练集比较大,一般 mini-batch 大小为 64~512(2 的次方比较好)
指数加权平均数 Exponentially Weighted Averages
为了更好了解接下来要介绍的优化算法,我们先要来看看指数加权平均数。

上图是某地某年的温度统计,左边是 1 月,右边是 12 月,蓝色的每个点代表每天的温度。红色的线就是其指数加权平均值,具体的公式为:
这里 $\theta_t$ 表示今天的温度,$v_t$ 表示计算出来的加权值,实际的含义我们可以认为是 $\frac{1}{a-\beta}$ 天的平均温度,比如红线可以看作是过去 10 天的平均值,如果 $\beta=0.98$,根据公式可知,对应的 $v_t$ 表示过去 50 天的平均温度,画出来就是绿色的线:

简单总结一下,$\beta$ 越大,曲线的波动越小,但是信息也越滞后。往往某个中间的值效果最好,具体需要试验得出。
指数加权平均数公式的好处之一是占用内存极少,基本只用一行代码和一点点内存
偏差修正 Bias Correction in Exponentially weighted averages
细心的同学可能会发现,当 $\beta=0.98$ 时相当于 50 天的平均值,那么绿线一开始怎么会和红线在差不多一样的高度呢?没错,如果我们直接用上一节的公式,算出来的曲线应该对应下图的紫线:

可以看到紫线的起点非常低,我们在预估初期不直接使用 $v_t$,而使用 $\frac{v_t}{1-\beta^t}$,就可以得到绿线。随着 t 不断增大,偏差修正也会越来越小,就和原来的一样了。
动量梯度下降法 Gradient descent with Momentum
简单来说,就是计算梯度的指数加权平均数,并以此更新权重,一般来说,动量梯度下降法的运行速度会比标准梯度下降法快。
我们来看下面一种情况:
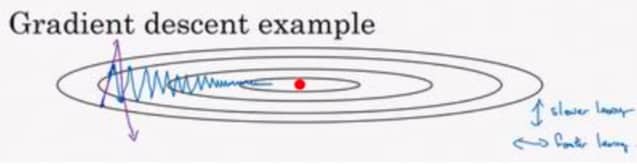
假设我们的优化过程如蓝线所示,一旦我们加大学习率,可能会偏离函数范围,所以我们不得不用比较小的学习率。总体来说,我们希望在垂直方向上少一点波动,而在水平方向上移动快一点。回忆一下前面的指数加权平均,我们是可以通过调整 $\beta$ 的值,来低效垂直方向上的波动的。具体的实现如下:

另外,有的时候 $1-\beta$ 部分会被去掉,不过具体怎么用可以自行决定
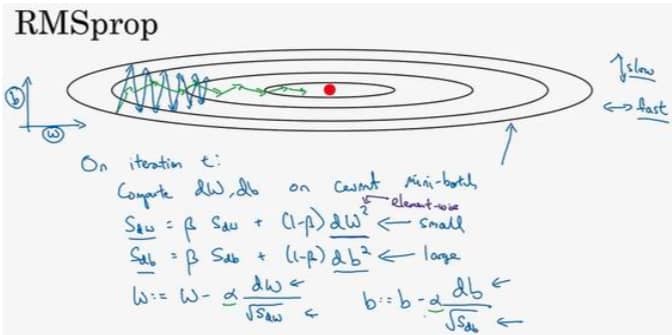
RMSprop
RMSprop 可以看作是动量梯度下降的一个改进,会让 W 方向的学习速度变快的同时,减少 b 方向的摆动。具体如下图所示:
Adam 优化算法
Adam 表示 Adaptive Moment Estimation,可以看作是 Momentum 和 RMSprop 合体的结果,能够有效适用于不同的神经网络,具体的公式推导这里不赘述,主要列举下关键参数的设置:
- $\alpha$: 学习率,需要自行调整
- $\beta_1$: 默认为 0.9,是 Momentum 涉及的项,一般不需要修改
- $\beta_2$: 默认为 0.999,是计算 $(dW)^2$ 和 $(db)^2$ 的移动加权平均,一般不需要修改
- $\epsilon$: 默认为 $10^{-8}$,一般不需要修改
学习率衰减 Learning Rate Decay
加快学习算法的另一个办法是随着时间慢慢减少学习率,简单理解就是一开始的尝试空间比较大,而后随着越来越接近最优,需要调整的就越小,如果还用一样大的学习率,就会反复横跳(如下图蓝线)。所以我们可以使学习率越来越小,达到绿线的效果,如下图所示:

具体的衰减方法有很多,比如指数衰减,基于 epoch 衰减,或离线下降衰减。但在诸多的超参数中,学习率衰减的优先级没有很高。
局部最优问题
简单来说,我们不太可能在优化的时候被困在极差的局部最优中,除非是训练存在大量参数且成本函数 J 被定义在较高维度空间的大型神经网络的时候。
相对来说,鞍点(见下图)是更容易出现的问题,需要特别注意选择合适的优化算法